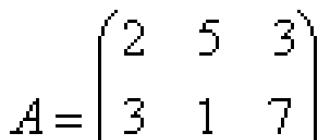В антагонистической игре произвольной размерности выигрыш первого. Основные понятия теории игр

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Введение

1. Теоретическая часть

1.3 Игра порядка 2х2

1.4 Алгебраический метод

1.5 Графический метод

1.6 Игры 2xn или mx2

1.7 Решения игр матричным методом

2. Практическая часть

2.2 Игры 2xn и mx2

2.3 Матричный метод

2.4 Метод Брауна

Анализ результатов

Введение

Антагонистическая игра - это игра с нулевой суммой. Антагонистической игрой называется некооперативная игра, в которой участвуют два игрока, выигрыши которых противоположны.

Формально антагонистическая игра может быть представлена тройкой , где X и Y -- множества стратегий первого и второго игроков, соответственно, F -- функция выигрыша первого игрока, ставящая в соответствие каждой паре стратегий (x,y), где действительное число, соответствующее полезности первого игрока при реализации данной ситуации.

Так как интересы игроков противоположны, функция F одновременно представляет и проигрыш второго игрока.

Исторически антагонистические игры являются первым классом математических моделей теории игр, при помощи которых описывались азартные игры. Считается, что благодаря этому предмету исследования теория игр и получила свое название. В настоящее время антагонистические игры рассматриваются как часть более широкого класса некооперативных игр.

1. Теоретическая часть

1.1 Основные определения и положения игры

Игра характеризуется системой правил, определяющих количество участников игры, их возможные действия и распределение выигрышей в зависимости от их поведения и исходов. Игроком принято считать одного участника или группу участников игры, имеющих одни общие для них интересы, не совпадающие с интересами других групп. Поэтому не каждый участник считается игроком.

Правила или условия игры определяют возможные поведения, выборы и ходы для игроков на любом этапе развития игры. Сделать выбор игроку, это значит остановиться на одной из его возможностей поведения. Затем игрок осуществляет этот выбор с помощью ходов. Сделать ход -- это значит на определенном этапе игры осуществить сразу весь выбор или его часть в зависимости от возможностей, предусмотренных правилами игры. Каждый игрок на определенном этапе игры делает ход согласно сделанному выбору. Другой игрок, зная или не зная о сделанном выборе первого игрока, также делает ход. Каждый из игроков старается учесть информацию о прошлом развитии игры, если такая возможность разрешается правилами игры.

Набор правил, которые однозначно указывают игроку, какой выбор он должен сделать при каждом ходе в зависимости от ситуации, сложившейся в результате проведения игры, называется стратегией игрока. Стратегия в теории игр означает определенный законченный план действий игрока, показывающий, как надо действовать ему во всех возможных случаях развития игры. Стратегия означает совокупность всех указаний для любого состояния информации, имеющейся у игрока на любом этапе развития игры. Отсюда уже видно, что стратегии могут быть хорошими и плохими, удачными и неудачными и т. д.

Игра с нулевой суммой будет тогда, когда сумма выигрышей всех игроков в каждой ее партии равна нулю, т. е. в игре с нулевой суммой общий капитал всех игроков не меняется, а перераспределяется между игроками в зависимости от получающихся исходов. Так, многие экономические и военные ситуации можно рассматривать как игры с нулевой суммой.

В частности игра двух игроков с нулевой суммой называется антагонистической, так как цели игроков в ней прямо противоположные: выигрыш одного игрока происходит только за счет проигрыша другого.

1.1.1 Определение, примеры и решения матричных игр в чистых стратегиях

Матричная игра двух игроков с нулевой суммой может рассматриваться как следующая абстрактная игра двух игроков.

Первый игрок имеет т стратегий i =1, 2,…, т, второй имеет п стратегий j = 1, 2,…, п. Каждой паре стратегий (i, j) поставлено в соответствие число a ij , выражающее выигрыш первого игрока за счет второго игрока, если первый игрок применит свою i-ю стратегию, а второй -- свою j-ю стратегию.

Каждый из игроков делает один ход: первый игрок выбирает свою i-ю стратегию (i =1, 2,…, т), второй --свою j-ю стратегию (j = 1, 2,…, п), после чего первый игрок получает выигрыш a ij за счет второго игрока (если a ij < 0, то это значит, что первый игрок платит второму сумму a ij). На этом игра заканчивается.

Каждая стратегия игрока i = 1, 2,…, т; j = 1, 2,…, п часто называется чистой стратегией.

Матричная игра двух игроков с нулевой суммой далее будет называться просто матричной игрой. Очевидно матричная игра относится к антагонистическим играм. Из ее определения следует, что для задания матричной игры достаточно задать матрицу А = (a ij) порядка тп выигрышей первого игрока.

Если рассмотреть матрицу выигрышей

то проведение каждой партии матричной игры с матрицей А сводится к выбору первым игроком i-й строки, а вторым игроком j-го столбца и получения первым игроком (за счет второго) выигрыша, находящегося в матрице А на пересечении i-й строки и j-го столбца.

Для формализации реальной конфликтной ситуации в виде матричной игры надо выделить и перенумеровать чистые стратегии каждого игрока и составить матрицу выигрышей.

Следующий этап -- это определение оптимальных стратегий и выигрышей игроков.

Главным в исследовании игр является понятие оптимальных стратегий игроков. В это понятие интуитивно вкладывается такой смысл: стратегия игрока является оптимальной, если применение этой стратегии обеспечивает ему наибольший гарантированный выигрыш при всевозможных стратегиях другого игрока. Исходя из этих позиций, первый игрок исследует матрицу А своих выигрышей по формуле (1.1) следующим образом: для каждого значения i (i =1, 2,…, т) определяется минимальное значение выигрыша в зависимости от применяемых стратегий второго игрока

(i = 1, 2,..., m) (1.2)

т. е. определяется минимальный выигрыш для первого игрока при условии, что он применит свою i - ю чистую стратегию, затем из этих минимальных выигрышей отыскивается такая стратегия i=i 0 , при которой этот минимальный выигрыш будет максимальным, т. е. находится

Определение. Число б, определенное по формуле (1.3), называется нижней чистой ценой игры и показывает, какой минимальный выигрыш может гарантировать себе первый игрок, применяя свои чистые стратегии при всевозможных действиях второго игрока.

Второй игрок при оптимальном своем поведении должен стремиться по возможности за счет своих стратегий максимально уменьшить выигрыш первого игрока. Поэтому для второго игрока отыскивается

т. е. определяется максимальный выигрыш первого игрока, при условии, что второй игрок применит свою j-ю чистую стратегию, затем второй игрок отыскивает такую свою j = j 1 стратегию, при которой первый игрок получит минимальный выигрыш, т. е. находит

Определение. Число в, определенное по формуле (1.5), называется чистой верхней ценой игры и показывает, какой максимальный выигрыш за счет своих стратегий может себе гарантировать первый игрок. Другими словами, применяя свои чистые стратегии первый игрок может обеспечить себе выигрыш не меньше б, а второй игрок за счет применения своих чистых стратегий может не допускать выигрыш первого игрока больше, чем в.

Определение. Если в игре с матрицей А нижняя и верхняя чистые цены игры совпадают, т. е. б = в, то говорят, что эта игра имеет седловую точку в чистых стратегиях и чистую цену игры:

н = б = в (1.6)

Седловая точка -- это пара чистых стратегий () соответственно первого и второго игроков, при которых достигается равенство

В понятие седловой точки вложен следующий смысл: если один из игроков придерживается стратегии, соответствующей седловой точке, то другой игрок не сможет поступить лучше, чем придерживаться стратегии, соответствующей седловой точке. Имея в виду, что лучшее поведение игрока не должно приводить к уменьшению его выигрыша, а худшее -- может приводить к уменьшению его выигрыша, эти условия можно записать математически в виде следующих соотношений:

где i, j -- любые чистые стратегии соответственно первого и второго игроков; (i 0 , j 0) -- стратегии, образующие седловую точку. Ниже будет показана эквивалентность определения седловой точки условиям (1.8).

Таким образом, исходя из (1.8), седловой элемент является минимальным в i 0 -й строке и максимальным в j 0 -м столбце в матрице А. Отыскание седловой точки матрицы А происходит легко: в матрице А последовательно в каждой строке находят минимальный элемент и проверяют, является ли этот элемент максимальным в своем столбце. Если он является таковым, то он и есть седловой элемент, а пара стратегий, соответствующая ему, образует седловую точку. Пара чистых стратегий (i 0 , j 0) первого и второго игроков, образующая седловую точку и седловой элемент называется решением игры.

Чистые стратегии i 0 и j 0 образующие седловую точку, называются оптимальными чистыми стратегиями соответственно первого и второго игроков.

Теорема 1. Пусть f (х, у) вещественная функция двух переменных х А и у В и существует

тогда б = в.

Доказательство. Из определения минимума и максимума следует, что

Поскольку в левой части (1.11) х любое, то

В правой части неравенства (1.12) у любое, поэтому

что и требовалось доказать.

В частности, матрица () есть частный случай функции f (х, у), т. е. если положить х = i, у = j, = f (х, у), то из теоремы 1 получим, что нижняя чистая цена не превосходит верхнюю чистую цену игры в матричной игре.

Определение. Пусть f (х, у) действительная функция двух переменных х А и у В. Точка (х 0 , у 0) называется седловой для функции f (х, у), если выполняются следующие неравенства

f (х, у 0) f (х 0 , у 0)f (х 0 , у) (1.14)

при любых х А и у В.

1.2 Оптимальные смешанные стратегии и их свойства

Исследование матричной игры начинается с нахождения ее седловой точки в чистых стратегиях. Если матричная игра имеет седловую точку в чистых стратегиях, то нахождением этой точки заканчивается исследование игры. Если же в матричной игре нет седловой точки в чистых стратегиях, то можно найти нижнюю и верхнюю чистые цены этой игры, которые указывают, что первый игрок не должен надеяться на выигрыш больший, чем верхняя цена игры, и может быть уверен в получении выигрыша не меньше нижней цены игры. Такие рекомендации относительно поведения игроков в матричной игре без седловой точки в чистых стратегиях не могут удовлетворять исследователей и практических работников. Улучшение решений матричных игр следует искать в использовании секретности применения чистых стратегий и возможности многократного повторения игр в виде партий. Так, например, проводится серия игр в шахматы, шашки, футбол, и каждый раз игроки применяют свои стратегии таким образом, что их противники не догадываются об их содержании, и на этом пути в среднем достигают определенных выигрышей, сыграв всю серию партий. Эти выигрыши в среднем больше нижней цены игры и меньше верхней цены игры. Чем больше это среднее значение, тем лучше стратегии применяет игрок. Поэтому возникла идея применять чистые стратегии случайно, с определенной вероятностью. Это полностью обеспечивает секретность их применения. Каждый игрок может изменять вероятности применения своих чистых стратегий таким образом, чтобы максимально увеличить свой средний выигрыш и на этом пути получать оптимальные стратегии. Такая идея привела к понятию смешанной стратегии.

Определение. Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий.

Таким образом, если первый игрок имеет т чистых стратегий 1, 2, … i,… m, то его смешанная стратегия х -- это набор чисел х = (х 1 , х 2 , ..., х i ,…, х т) удовлетворяющих соотношениям

x i 0 (i = 1, 2, ... , т), = 1. (1.15)

Аналогично для второго игрока, который имеет п чистых стратегий, смешанная стратегия у -- это набор чисел у = (у 1 ,…, у j , … у n), удовлетворяющих соотношениям

y j 0 (j = 1, 2, ... , n), = 1. (1.16)

Так как каждый раз применение игроком одной чистой стратегии исключает применение другой, то чистые стратегии являются несовместимыми событиями. Кроме того, они являются единственно возможными событиями.

Очевидно, чистая стратегия есть частный случай смешанной стратегии. Действительно, если в смешанной стратегии какая-либо i-я чистая стратегия применяется с вероятностью единица, то все остальные чистые стратегии не применяются. И эта i-я чистая стратегия является частным случаем смешанной стратегии. Для соблюдения секретности каждый игрок применяет свои стратегии независимо от выбора другого игрока.

Определение. Средний выигрыш первого игрока в матричной игре с матрицей А выражается в виде математического ожидания его выигрышей

Е (А, х, у)= (1.20)

Очевидно, средний выигрыш первого игрока есть функция двух наборов переменных х и у. Первый игрок имеет целью за счет изменения своих смешанных стратегий х максимально увеличить свой средний выигрыш Е (А, х, у), а второй -- за счет своих смешанных стратегий стремится сделать Е (А, х, у) минимальным, т. e. для решения игры необходимо найти такие х, у, при которых достигается верхняя цена игры.

1.3 Игра порядка 22

Матричная игра порядка 22 задается следующей матрицей выигрышей первого игрока:

Решение этой игры следует начинать с отыскания седловой точки в чистых стратегиях. С этой целью находят минимальный элемент в первой строке и проверяют, является ли он максимальным в своем столбце. Если такого элемента не нашли, то аналогично проверяют вторую строку. Если во второй строке такой элемент найден, то он является седловым.

Отысканием седлового элемента, если такой имеется, заканчивается процесс нахождения ее решения, так как в этом случае найдена цена игры --седловой элемент и седловая точка, т. е. пара чистых стратегий, для первого и второго игрока, составляющих оптимальные чистые стратегии. Если же седловой точки в чистых стратегиях не оказалось, то надо отыскать седловую точку в смешанных стратегиях, которая обязательно существует согласно основной теореме матричных игр.

Обозначим через х=(х 1 ,х 2), у=(у 1 ,у 2) смешанные стратегии соответственно первого и второго игроков. Напомним, что х 1 означает вероятность применения первым игроком своей первой стратегии, а х 2 = 1 - х 1 - вероятность применения им своей второй стратегии. Аналогично для второго игрока: у 1 - вероятность применения им первой стратегии, у 2 = 1 - у 1 - вероятность применения им второй стратегии.

Согласно следствию из теореме, для оптимальности смешанных стратегий х и у необходимо и достаточно, чтобы для неотрицательных х 1 , х 2 , у 1 , у 2 выполнялись следующие соотношения:

Покажем теперь, что если матричная игра не имеет седловой точки в чистых стратегиях, то эти неравенства должны превращаться в равенства:

В самом деле. Пусть игра не имеет седловой точки в чистых стратегиях, тогда оптимальные значения смешанных стратегий удовлетворяют неравенствам

0<<1, 0<< 1,

0< <1, 01. (1.25)

Предположим, что оба неравенства из (1.22) будут строгими

тогда согласно теореме должно у 1 = у 2 = 0, что противоречит условиям (1.25).

Аналогично доказывается, что оба неравенства из (1.23) не могут быть строгими неравенствами.

Предположим теперь, что одно из неравенств (1.22) может быть строгим, например первое

Это значит, что согласно теореме у 1 = 0, у 2 =1. Следовательно, из (1.23) получаем

Если оба неравенства (1.24) строгие, то по теореме должно х 1 = х 2 = 0, что противоречит (1.25). Если же а 12 а 22 , то одно из неравенств (1.27) строгое, а другое -- равенство. Причем равенство будет выполняться для большего элемента из а 12 и а 22 , т. е. одно неравенство из (1.27) должно быть строгим. Например а 12 < а 22 . Тогда справедливо а 12 < v, а это равносильно тому, что первое неравенство из (1.24) строгое. Тогда согласно теореме должно х 1 = 0, что противоречит условию (1.25). Если а 12 = а 22 , то оба неравенства (1.27) превращаются в равенства и тогда можно положить х 1 = 0, что противоречит (1.25). Итак, предположение о том, что первое неравенство из (1.22) может быть строгим, не справедливо. Аналогично можно показать, что второе неравенство из (1.22) также не может быть строгим.

Таким образом показано, что если матричная игра не имеет седловой точки в чистых стратегиях, то для оптимальных стратегий первого игрока неравенства (1.22) превращаются в равенства. Аналогичные рассуждения относительно неравенств (1.23) приведут к тому, что в этом случае неравенства (1.23) должны быть равенствами.

Итак, если матричная игра порядка 22 не имеет седловой точки, то оптимальные смешанные стратегии игроков и цену игры можно определить, решив систему уравнений (1.24). Установлено также, что если в матричной игре порядка 2x2 один из игроков имеет оптимальную чистую стратегию, то и другой игрок также имеет оптимальную чистую стратегию.

Следовательно, если матричная игра не имеет седловой точки в чистых стратегиях, то она должна иметь решение в смешанных стратегиях, которые определяются из уравнений (1.24). Решение системы (1.25)

1.4 Алгебраический метод

Возможны два случая для решения задач алгебраическим методом:

1. матрица имеет седловую точку;

2. матрица не имеет седловую точку.

В первом случае решение - это пара стратегий, образующих седловую точку игры. Рассмотрим второй случай. Решения здесь следует искать в смешанных стратегиях:

Отыщем стратегии и. При использовании первым игроком своей оптимальной стратегии второй игрок может, например, применить две такие чистые стратегии

При этом в силу свойства, если один из игроков применяет оптимальную смешанную стратегию, а другой - любую чистую, входящую в его оптимальную смешанную стратегию с вероятностью не равной нулю, то математическое ожидание выигрыша всегда остается неизменным и равным цене игры, т.е.

Выигрыш должен в каждом из этих случаев быть равен цене игры V. В таком случае справедливы такие соотношения:

Систему уравнений, аналогичную (2.5), (2.6) можно составить и для оптимальной стратегии второго игрока:

Принимая во внимание условие нормировки:

Решим совместно уравнение (1.37) - (1.41) относительно неизвестных можно решать и не все сразу, а по три: отдельно (1.36), (1.38), (1.40) и (1.37), (1.39), (1.41). В результате решения получим:

1.5 Графический метод

Приближенное решение игры 22 можно довольно просто получить воспользовавшись графическим методом. Суть его заключается в следующем:

Рисунок 1.1- нахождение участка единичной длинны

Выделить на оси абсцисс участок единичной длины. Левый конец его будет изображать первую стратегию первого игрока, а правый вторую. Все промежуточные точки соответствуют смешанным стратегиям первого игрока, причем длина отрезка справа от точки равна вероятности применения первой стратегии, а длина отрезка слева от - вероятности применения второй стратегии первым игроком.

Проведены две оси I-I и II-II. На I-I будем откладывать выигрыш при использовании первым игроком первой стратегии, на II-II при использовании им второй стратегии. Пусть, например, второй игрок применил свою первую стратегию, тогда на оси I-I следует отложить величину, а на оси II-II - величину

При любой смешанной стратегии первого игрока его выигрыш определится величиной отрезка. Линия I-I соответствует применению первой стратегии вторым игроком, будем её называть первой стратегией второго игрока. Аналогично можно построить и вторую стратегию второго игрока. Тогда в целом графическое отображение матрицы игры примет такой вид:

Рисунок 1.2 - нахождение цены игры

Следует однако отметить, что это построение проводилось для первого игрока. Здесь длина отрезка ровна цене игры V.

Линия 1N2 называется нижней границей выигрыша. Здесь наглядно видно, что точка N соответствует максимальной величине гарантированного выигрыша первого игрока.

Вообще то говоря, стратегию второго игрока также можно определить из этого рисунка, например такими способами. На оси I-I:

либо на оси II-II

Однако стратегию второго игрока можно определить и аналогично тому, как это делается для первого игрока, т.е. построить такой график.

Рисунок 1.3 - определение стратегии второго игрока

Здесь линия 1N2 - верхняя граница проигрыша. Точка N соответствует минимальному из возможных проигрышей второго игрока, она то и определяет стратегию.

В зависимость от конкретных значений коэффициентов матрицы графика могут иметь и иной вид, например, такой:

Рисунок 1.4 - определяет оптимальную стратегию первого игрока

В такой ситуации оптимальная стратегия первого игрока является чистой:

1.6 Игры 2n или m2

В играх порядка 2n первый игрок имеет 2 чистых стратегии, а второй n чистых стратегий, т.е. матрица выигрышей первого игрока имеет вид:

Если такая игра имеет седловую точку, то её легко найти и получить решение.

Предположим, что игра имеет седловые точки. Тогда необходимо найти такие смешанные стратегии и соответственно первого и второго игроков и цену игры v, которые удовлетворяют соотношениям:

Поскольку игра не имеет седловой точки, то неравенство (1.54) заменяют не равенствами

Для решения систем (1.56), (1.55), (1.53) целесообразно воспользоваться графическим методом. С целью введем обозначения для левой части неравенства (1.53)

матричный игра математический модель

или, поставив из (1.55) и проведя простые преобразования, получим

где - это средний выигрыш первого игрока при условии, что он применяет свою смешанную стратегию, а второй свою j-ю чистую стратегию.

Каждому значению j=1, 2, … , n согласно выражению соответствует прямая линия в прямоугольной системе координат.

Цель второго игрока минимизировать выигрыш первого игрока за счет выбора своих стратегий. Поэтому вычисляем

где - нижняя граница множества ограничений. На рисунке 1.6 график функции изображен жирной линей.

Размещено на http://www.allbest.ru/

Рисунок 1.6 - график функции

Цель первого игрока максимизировать свой выигрыш за счет выбора, т.е. вычислить

На рисунке 1.6 точка означает максимальное значение, которое получается при. Цена игры, так как:

Таким образом графически определяется оптимальная смешанная стратегия первого игрока и пара чистых стратегий второго игрока, которые в пересечении образуют точку На рисунке 1.6 изображены 2-я и 3-я стратегия второго игрока. Для таких стратегий неравенства (1.53) превращаются в равенства. На рисунке 1.6 это стратегии j=2, j=3.

Теперь можно решить систему уравнений

и точно определить значения и (графически они определяются приближенно). Затем положив все значения при тех j, для которых не образуют точку, решая систему уравнений (1.56) Для примера, приведенного на рисунке 1.6, это следующая система:

а остальные Эту систему можно решить, пологая Если при некоторой j=j 0 стратегии второго игрока образуют точку М 0 и то максимальное значение нижней границы множеств ограничений изображается отрезком, параллельным оси В этом случае первый игрок имеет бесконечно много оптимальных значений а цена игры Этот случай изображен на рисунке 1.7, где и отрезок MN изображают верхнее ограничений, оптимальные значения находятся в пределах У второго игрока имеется чистая оптимальная стратегия j=j 0 .

Матричные игры порядка m2 решаются также с помощью графического метода. Матрица выигрышей первого игрока в этом случае имеет вид

Смешанные стратегии соответственно первого и второго игроков определяются аналогично, как в случае игр порядка 2n. Пусть по горизонтальной оси откладывается значение от 0 до 1, по вертикальной - значение среднего выигрыша) первого игрока при условиях, что первый игрок применяет свою чистую i-ю стратегию (i=1, 2, …, m), второй - свою смешанную стратегию (y 1 , 1- y 1) =y. Например, при m=4 графически) могут быть представлены так, как изображено на рисунке 1.7.

Рисунок 1.7 - график функции)

Первый игрок старается максимизировать свой средний выигрыш, поэтому он стремиться найти

Функция изображена жирной линей и представляет собой верхнюю границу множества ограничений. Второй игрок старается минимизировать за счет выбора своей стратегии, т.е. величина соответствует

На рисунке значение обозначено точкой. Другими словами определяются такие две стратегии первого игрока и вероятность для второго игрока, при которых достигается равенство

Из рисунка видим, что цена игры - это ордината точки, вероятность - это абсцисса точки. Для остальных чистых стратегий первого игрока в оптимальной смешанной стратегии должно ().

Таким образом, решая систему (1.69), получим оптимальную стратегию второго игрока и цену игры. Оптимальную смешанную стратегию для первого игрока найдем, решая следующую систему уравнений:

1.7 Матричный метод решения игр

Обозначения:

Любая квадратная подматрица матрицы порядка

Матрица (1);

Матрица, транспонированная к;

Матрица, присоединенная к В;

- (1) матрица полученная из X вычеркиванием элементов, которые соответствуют строкам, вычеркнутым из при получении;

- (1) матрица полученная из вычеркиванием элементов, которые соответствуют строкам, вычеркнутым из при получении.

Алгоритм:

1. Выберем квадратную подматрицу матрицы порядка () и вычислим

2. Если некоторое или, то отбрасываем найденную матрицу и пробуем другую матрицу.

3. Если (), (), вычисляем и строим X и из и, добавляя в соответствующих местах нули.

Проверяем, удовлетворяются ли неравенства

для каждого (1.75)

и неравенства

для каждого (1.76)

Если одно из соотношений не выполнено, то пробуем другое. Если все соотношения справедливы, то X, и искомые решения.

1.8 Метод последовательного приближения цены игры

При исследовании игровых ситуаций часто может случиться так, что нет необходимости в получении точного решения игры или в следствии каких-либо причин найти точное значение цены игры и оптимальных смешанных стратегий невозможно или очень трудно. Тогда можно воспользоваться приближенным методами решения матричной игры.

Опишем один из таких методов - метод последовательного приближения цены игры. Количество вычисленных при использовании метода увеличивается примерно пропорционально числу строк и столбцов матрицы выигрышей.

Сущность метода состоит в следующем: мысленно игра проводится много раз, т.е. последовательно, в каждой партии игры игрок выбирает ту стратегию, которая дает ему наибольший общий (суммарный) выигрыш.

После такой реализации некоторых партий вычисляет средние значение выигрыша первого игрока, проигрыша второго игрока, и их среднее арифметическое принимается за приближенное значение цены игры. Метод дает возможность найти приближенное значение оптимальных смешанных стратегий обоих игроков: надо подсчитать частоту применения каждой чистой стратегии и принять её за приближенное значение в оптимальной смешанной стратегии соответствующего игрока.

Можно доказать, что с неограниченным увеличением числа программных партий средний выигрыш первого игрока и средний проигрыш второго игрока будет неограниченно приближаться к цене игры, а приближенные значения смешанных стратегий в том случае, когда решение игры единственное, будет стремиться к оптимальным смешанным стратегиям каждого игрока. Вообще говоря, стремление приближенных значений выше указанных величин к истинным значениям происходит медленно. Однако этот процесс легко механизировать и тем самым помочь получению решения игры с требуемой степенью точности даже при матрицах выигрышей сравнительно большого порядка.

2. Практическая часть

Пара решает куда пойти погулять и с пользой для двоих провести время.

Девушка решает пойти погулять в парк подышать свежим воздухом, вечером сходить на просмотр кинофильма в ближайший кинотеатр.

Парень предлагает пойти сходить в технопарк, после посмотреть матч футболистов местного клуба в центральном стадионе.

В соответствии с этим нужно найти за какое время будет достигнута цель одного из игроков. Матрица выигрышей будет выглядеть таким образом:

Таблица 1. Матрица выигрышей

Стратегии

Так как 1 2 , Очевидно, в этой игре нет седловой точки в чистых стратегиях. Поэтому воспользуемся следующими формулами, и получим:

Размещено на http://www.allbest.ru/

2.2 Игра 2xn и mx2

Задача 1(2xn)

Выращивается две зерновые культуры для сухого и влажного климата.

А состояние природы можно рассматривать как: сухое, влажное, умеренное.

Размещено на http://www.allbest.ru/

Максимальное значение М() достигается в точке М, образуемой пересечением линий, соответствующих j=1, j"=2. По этому полагаем: ,

Задача 2(mx2)

Парень и девушка рассматривают варианты куда пойти на выходные.

Выбор места отдыха можно представить как: парк, кино, рессторан.

Размещено на http://www.allbest.ru/

Максимальное значение М() достигается в точке E, образуемой пересечением линий, соответствующих j=1, j"=2. По этому полагаем: ,

Для определения значения, v надо решить следующие уравнения:

2.5 Матричный метод

Два конкурирующих друг с другом ресторана(предприятия общественного питания) предоставляют следующие наборы услуг. Первый ресторан расположен в центре, а другая на окраине города.

Центральный ресторан включает следующие услуги:

1) более дорогое и качественное обслуживание клиентов;

2) блюда ориентированы на французскую кухню;

Второй ресторан предоставляет:

1) не дорогое и качественное обслуживание;

2) меню сочетает в себе различные известные кухни мира;

3) также постоянные акции и скидки;

4) осуществляет доставку и принимает заказы по доставке на дом.

В соответствии с заданием прибыль за один день между двумя ресторанами распределится следующим образом:

Таблица 2. Матрица выигрышей

Стратегии

Решение игры вида матричным способом:

Существует шесть подматриц и:

Рассмотрим матрицу:

x 1 = ? 0, x 2 = ? 0

Так как x 2 = < 0, то мы отбрасываем.

Рассмотрим теперь матрицу:

x 1 = ? 0, x 2 = ? 0

Цена игры.

Это соотношение противоречит требованию, поэтому не подходит.

Рассмотрим теперь матрицу:

x 1 = , x 2 = ? 0,

y 1 = < 0, y 2 = ? 0.

Так как y 1 = < 0, то мы отбрасываем и.

Рассмотрим теперь матрицу:

x 1 = , x 2 = 0, так как x 2 = 0, то мы отбрасываем и.

Рассмотрим теперь матрицу:

x 1 = , x 2 = ? 0. Так как x 1 = 0, то мы отбрасываем и.

Рассмотрим теперь матрицу:

x 1 = , x 2 =, y 1 = , y 2 =, то продолжаем дальше:

x 1 = , x 2 =, y 1 = , y 2 = или

Цена игры.

Теперь проверяются основные соотношения:

Размещено на http://www.allbest.ru/

Ответ: x 1 = , x 2 =, y 1 = , y 2 = , y 3 =0, y 4 =0,.

Метод Брауна

По требованию рабочих некоторой компании профсоюз ведет с ее руководством переговоры об организации горячих обедов за счет компании. Профсоюз, представляющий интересы рабочих, добивается того, чтобы обед был как можно более качественным и, следовательно, более дорогим. Руководство компании имеет противоположные интересы. В конце концов стороны договорились о следующем. Профсоюз (игрок 1) выбирает одну из трех фирм (А 1 , А 2 , А 3), поставляющих горячее питание, а руководство компании (игрок 2) -- набор блюд из трех возможных вариантов (B 1 , B 2 , B 3). После подписания соглашения профсоюз формирует следующую платежную матрицу, элементы которой представляют стоимость набора блюд:

Пусть игра задана следующей матрицей выигрышей:

Предположим, что второй игрок выбрал свою 2-ю стратегию, тогда первый получит:

2, если он применит свою 1-ю стратегию,

3, если он применит свою 3-ю стратегию.

Полученные значения сводится в таблицу 1.

Таблица 3. Стратегия второго игрока

№ партии	Стратегия 2-го игрока	Выигрыш 1-го игрока

Из таблицы 3 видно, что при 2-й стратегии второго игрока первый получит наибольший выигрыш 3, используя свою 2-ю либо 3-ю стратегию. Поскольку первый игрок желает получить максимальный выигрыш, то он на 2-ю стратегию второго игрока отвечает своей 2-й стратегией. При 2-й стратегии первого игрока второй проиграет:

1, если он применит свою 1-ю стратегию,

3, если он применит свою 2-ю стратегию,

4, если он применит свою 3-ю стратегию.

Таблица 4. Стратегия первого игрока

№ партии	Стратегия 1-го игрока	Проигрыш 2-го игрока

Из таблицы 2 видно, что при 2-й стратегии первого игрока второй игрок будет иметь наименьший проигрыш 1, если он применит свою 1-ю стратегию. Поскольку второй игрок желает проиграть меньше, то в ответ на 2-ю стратегию первого игрока он применит свою 1-ю стратегию. Полученные результаты сводятся в таблицу 5.

Таблица 5. Стратегии соответственно первого и второго игроков

№ партии

Стратегия 2-го игрока

Суммарный выигрыш 1-го игрока

Стратегия 1-го игрока

В табл. 5 в столбце стратегии второго игрока во второй строке находится цифра 1, которая указывает, что во второй партии второму игроку выгодно применять свою 1-ю стратегию; в столбце и находится наибольший средний выигрыш 3 первого игрока, полученный им в первой партии; в столбце w стоит наименьший средний проигрыш 1, полученный вторым игроком в первой партии; в столбце v находится среднее арифметическое v = (и + w) -- т. е. приближенное значение цены игры, полученное в результате проигрывания одной партии игры. Если второй игрок применит свою 1-ю стратегию, то первый получит 3, 1, 2 соответственно при своих 1-й, 2-й, 3-й стратегиях, а суммарный выигрыш первого игрока за обе партии составит:

2 + 3=5 при его 1-й стратегии,

3 + 1=4 при его 2-й стратегии,

3 + 2=5 при его 3-й стратегии.

Эти суммарные выигрыши записываются во второй строке табл. 3 и в столбцах, соответствующих стратегиям первого игрока: 1, 2, 3.

Из всех суммарных выигрышей наибольшим является 5. Он получается при 1-й и 3-й стратегии первого игрока, то ему можно выбирать любую из них; скажем, в таких случаях, когда имеются два (или несколько) одинаковых суммарных выигрышей, выбирают стратегию с наименьшим номером (в нашем случае надо взять 1-ю стратегию).

При 1-й стратегии первого игрока второй проиграет 3, 2, 3 соответственно 1-й, 2-й, 3-й его стратегиям, а суммарный проигрыш второго игрока за обе партии составит:

1 + 3=4 при его 1-й стратегии,

3 + 2=5 при его 2-й стратегии,

4 + 3=7 при его 3-й стратегии.

Эти суммарные проигрыши записываются во второй строке табл. 5 и в столбцах, соответствующих 1-й, 2-й, 3-й стратегиям второго игрока.

Из всех суммарных проигрышей второго игрока наименьшим является 4. Он получается при его 1-й стратегии, следовательно, в третьей партии второй игрок должен применить свою 1-ю стратегию. В столбец и ставится наибольший суммарный выигрыш первого игрока за две партии, деленный на число партий, т. е. ; в столбец w ставится наименьший суммарный проигрыш второго игрока за две партии, деленный на число партий, т. е. ; в столбце v ставится среднее арифметическое этих значений, т. е. = Это число принимается приближенное значение цены игры при двух «сыгранных» партиях.

Таким образом, получается следующая таблица 4, для двух партий игры.

Таблица 6. Суммарные выигрыш и проигрыш игроков при двух сыгранных партиях

Стратегия 2-го игрока

Суммарный выигрыш 1-го игрока

Стратегия 1-го игрока

Суммарный проигрыш 2-го игрока

В третьей строке таблицы 6 в столбце стратегии второго игрока находится число 1, которое показывает, что в третьей партии второй игрок должен применить свою 1-ю стратегию. В этом случае первый игрок выигрывает 3, 1, 2, используя соответственно свои 1-ю, 2-ю, 3-ю стратегии, а его суммарный выигрыш за три партии составит:

3 + 5 = 8 при его 1-й стратегии,

1 +4 = 5 при его 2-й стратегии,

2 + 5 = 7 при его 3-й стратегии.

Эти суммарные выигрыши первого игрока записываются в третьей строке таблица 6 и столбцах, соответствующих его стратегиям 1, 2, 3. Так как наибольший суммарный выигрыш 8 первого игрока получается при 1-й стратегии, соответственно выбирает 1-ю.

При 1-й стратегии первого игрока второй проиграет 3, 1, 2 соответственно 1-й, 2-й, 3-й его стратегиям, а суммарный проигрыш второго игрока за обе партии составит:

3 + 4=7 при его 1-й стратегии,

2 + 5=7 при его 2-й стратегии,

3 + 7=10 при его 3-й стратегии.

Эти суммарные проигрыши записываются во третьей строке табл. 6 и в столбцах, соответствующих 1-й, 2-й, 3-й стратегиям второго игрока. Из всех суммарных его проигрышей 7 является наименьшим и получается при его 1-й и 2-й стратегиях, далее второму игроку надо применить свою 1-ю стратегию.

В табл. 6 в третьей строке в столбце и записывается наибольший суммарный выигрыш первого игрока за три партии, деленный на число партии, т. е. ; в столбце w ставится наименьший суммарный проигрыш второго игрока за три партии, деленный на число партий, т. е. ; в столбце v ставится их среднее арифметическое

Таким образом получаем табл. 7 для трех партий.

Таблица 7. Суммарные выигрыш и проигрыш игроков при трех сыгранных партиях

№ партии

Стратегия 2-го игрока

Суммарный выигрыш 1-го игрока

Стратегия 1-го игрока

Суммарный проигрыш 2-го игрока

Таблица 8. Конечная таблица при двадцати сыгранных партиях

№ партии

Стратегия 2-го игрока

Суммарный выигрыш 1-го игрока

Стратегия 1-го игрока

Суммарный проигрыш 2-го игрока

Из табл. 7 и 8 видно, что в 20-ти проигранных партиях стратегии 1, 2, 3 для первого игрока встречаются соответственно 12, 3, 5 раз, следовательно, их относительные частоты соответственно равны; стратегии 1, 2, 3 для второго игрока встречаются соответственно 7, 11,2 раза, следовательно их относительные частоты соответственно равны; приближенное значение цены игры. Такое приближение достаточно хорошее.

В заключение отметим, что, если игра имеет больше одного решения, то приближенные значения цены игры по-прежнему будут неограниченно приближаться к истинной цене игры, а относительные частоты появления стратегий игроков уже не обязательно будут приближаться к истинным оптимальным смешанным стратегиям игроков.

Анализ результатов

В данной курсовой работе изучен материал нахождения решения антагонистических игр графическим, матричным методом, методом последовательного приближения цены игры. Найдены оптимальные стратегии первого и второго игрока, а также цена игры в играх 2x2, 2xn и mx2, а так же в играх с использованием матричного метода и метода Брауна.

На примере пары была смоделирована игра 2x2, которая была решена алгебраическим и графическим методом. Решая игру алгебраическим методом решение показывает, что применяя свои оптимальные смешанные стратегии первый и второй игрок проведут вместе 4.6 часа. Графическое решение задачи получилось с небольшой погрешностью и составило 4.5 часа.

А так же были смоделированы две задачи 2xn и mx2. В задаче 2xn была рассмотрена с/х культура и стратегия показывает, что лучше поле засадить 50 на 50, а цена игры составила 3.75 млн. рублей. А в задаче mx2 была рассмотрена пара, стратегия которой показала, что дешевле пойти в парк и кино, а цена затраты составят 4.3 рублей.

Была смоделирована задача для матричного метода, в которой рассматривались два ресторана, решение задачи показало, что при применение свой оптимальной смешанной стратегии прибыль первого ресторана составит 15.6 млн. рублей, а при использовании своей оптимальной смешанной стратегии вторым рестораном, он не позволит первому заработать больше 15.6 млн. рублей. Решение графическим методом дало погрешность и цена игры составила 14.9 млн. рублей.

Для метода Брауна была составлена задача в которой рассматривается профсоюз и руководство компании, их задача обеспечить питание рабочих. При использовании обоими игроками своих оптимальных стратегий питание на человека составит 2.45 тыс. руб.

Список использованных источников

1) Вилисов В.Я. Конспект лекций «Теория игр и статистических решений», - Филиал - «Восход» МАИ. 1979. 146 с.

2) Крушевский А.В. Теория игр, - Киев: Вища школа, 1977. - 216 с.

3) Черчмень У., Акоф Р., Арноф Л., Введение в исследование операций. - М.: Наука. 1967. - 488 с.

4) http://www.math-pr.com/exampl_gt2.htm

5) http://ru.wikipedia.org/wiki/%D0%90%D0%BD%D1% 82%D0%B0%D0 %B3%D0%BE%D0%BD%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%B8%D0%B3%D1%80%D0%B0

Размещено на Allbest.ru

Подобные документы

Принятие решений как особый вид человеческой деятельности. Рациональное представление матрицы игры. Примеры матричных игр в чистой и смешанной стратегиях. Исследование операций: взаимосвязь задач линейного программирования с теоретико-игровой моделью.

курсовая работа , добавлен 05.05.2010

Игры, повторяемые многократно, их отличительные свойства и этапы. Смешанные стратегии, условия и возможности их использования на практике. Аналитический метод решения игры типа 2 x 2. Основные теоремы для прямоугольных игр. Алгебраические решения.

презентация , добавлен 23.10.2013

Основные определения теории биматричных игр. Пример биматричной игры "Студент-Преподаватель". Смешанные стратегии в биматричных играх. Поиск "равновесной ситуации". 2x2 биматричные игры и формулы для случая, когда у каждого игрока имеется две стратегии.

реферат , добавлен 13.02.2011

Изучение общих сведений о матричных и антагонистических играх. Понятие позиционной игры, дерева, информационного множества. Рассмотрение принципа максимина и принципа равновесия. Оптимальность по Парето. Позиционная неантагонистическая игра, ее свойства.

курсовая работа , добавлен 17.10.2014

Теория игр – раздел математики, предметом которого является изучение математических моделей принятия оптимальных решений в условиях конфликта. Итеративный метод Брауна-Робинсона. Монотонный итеративный алгоритм решения матричных игр.

дипломная работа , добавлен 08.08.2007

Составление платежной матрицы, поиск нижней и верхней чисты цены игры, максиминной и минимаксной стратегии игроков. Упрощение платежной матрицы. Решение матричной игры с помощью сведения к задаче линейного программирования и надстройки "Поиск решения".

контрольная работа , добавлен 10.11.2014

Теория игр - математическая теория конфликтных ситуаций. Разработка математической модели игры двух лиц с нулевой суммой, ее реализация в виде программных кодов. Метод решения задачи. Входные и выходные данные. Программа, руководство пользователя.

курсовая работа , добавлен 17.08.2013

Основные сведения о симплекс-методе, оценка его роли и значения в линейном программировании. Геометрическая интерпретация и алгебраический смысл. Отыскание максимума и минимума линейной функции, особые случаи. Решение задачи матричным симплекс-методом.

дипломная работа , добавлен 01.06.2015

Приемы построения математических моделей вычислительных систем, отображающих структуру и процессы их функционирования. Число обращений к файлам в процессе решения средней задачи. Определение возможности размещения файлов в накопителях внешней памяти.

лабораторная работа , добавлен 21.06.2013

Проектирование математической модели. Описание игры в крестики-нолики. Модель логической игры на основе булевой алгебры. Цифровые электронные устройства и разработка их математической модели. Игровой пульт, игровой контроллер, строка игрового поля.

Рассмотрим конечную парную игру с нулевой суммой. Обозначим через a выигрыш игрока A , а через b – выигрыш игрока B . Так как a = –b , то при анализе такой игры нет необходимости рассматривать оба этих числа – достаточно рассматривать выигрыш одного из игроков. Пусть это будет, например, A . В дальнейшем для удобства изложения сторону A будем условно именовать "мы ", а сторону B – "противник ".

Пусть у нас имеется m возможных стратегийA 1 , A 2 , …, A m , а у противника n возможных стратегий B 1 , B 2 , …, B n (такая игра называется игрой m×n ). Предположим, что каждая сторона выбрала определенную стратегию: мы выбрали A i , противник B j . Если игра состоит только из личных ходов, то выбор стратегий A i и B j однозначно определяет исход игры – наш выигрыш (положительный или отрицательный). Обозначим этот выигрыш через a ij (выигрыш при выборе нами стратегии A i , а противником – стратегии B j ).

Если игра содержит кроме личных случайные ходы, то выигрыш при паре стратегий A i , B j есть величина случайная, зависящая от исходов всех случайных ходов. В этом случае естественной оценкой ожидаемого выигрыша является математическое ожидание случайного выигрыша . Для удобства будем обозначать через a ij как сам выигрыш (в игре без случайных ходов), так и его математическое ожидание (в игре со случайными ходами).

Предположим, что нам известны значения a ij при каждой паре стратегий. Эти значения можно записать в виде матрицы, строки которой соответствуют нашим стратегиями (A i ), а столбцы – стратегиям противника (B j ):

B j A i	B 1	B 2	…	B n
A 1	a 11	a 12	…	a 1n
A 2	a 21	a 22	…	a 2n
…	…	…	…	…
A m	a m 1	a m 2	…	a mn

Такая матрица называется платежной матрицей игры или просто матрицей игры .

Заметим, что построение платежной матрицы для игр с большим количеством стратегий может представлять непростую задачу. Например, для шахматной игры число возможных стратегий так велико, что построение платежной матрицы является практически неосуществимым. Однако, в принципе любая конечная игра может быть приведена к матричной форме.

Рассмотрим пример 1 антагонистической игры 4×5. В нашем распоряжении есть четыре стратегии, у противника – пять стратегий. Матрица игры следующая:

B j A i	B 1	B 2	B 3	B 4	B 5
A 1
A 2
A 3
A 4

Какой стратегией нам (т.е. игроку A ) воспользоваться? Какую бы мы ни выбрали стратегию, разумный противник ответит на нее той стратегией, для которой наш выигрыш будет минимальным. Например, если мы выберем стратегию A 3 (соблазнившись выигрышем 10), противник в ответ выберет стратегию B 1 , и наш выигрыш будет всего лишь 1. Очевидно, исходя из принципа осторожности (а он – основной принцип теории игр), надо выбирать ту стратегию, при которой наш минимальный выигрыш максимален .

Обозначим через α i минимальное значение выигрыша для стратегии A i :

и добавим к матрице игры столбец, содержащий эти значения:

B j A i	B 1	B 2	B 3	B 4	B 5	минимум в строках α i
A 1
A 2
A 3
A 4							максимин

Выбирая стратегию, мы должны предпочесть ту, для которой значение α i максимально. Обозначим это максимальное значение через α :

Величина α называется нижней ценой игры или максимином (максимум минимального выигрыша). Стратегия игрока A , соответствующая максимину α , называется максиминной стратегией .

В данном примере максимин α равен 3 (соответствующая клетка в таблице выделена серым цветом), а максиминная стратегия –A 4 . Выбрав эту стратегию, можем быть уверены, что при любом поведении противника выиграем не меньше, чем 3 (а может быть и больше при "неразумном" поведении противника"). Эта величина – наш гарантированный минимум, который мы можем себе обеспечить, придерживаясь наиболее осторожной ("перестраховочной") стратегии.

Теперь проведем аналогичные рассуждения за противника B B A B 2 – мы ему ответим A .

Обозначим через β j A B ) для стратегии A i :

β j β :

7.ЧТО НАЗЫВАЕТСЯ ВЕРХНЕЙ ЦЕННОЙ ИГРЫТеперь проведем аналогичные рассуждения за противника B . Он заинтересован в том, чтобы обратить наш выигрыш в минимум, то есть отдать нам поменьше, но должен рассчитывать на наше, наихудшее для него, поведение. Например, если он выберет стратегию B 1 , то мы ответим ему стратегией A 3 , и он отдаст нам 10. Если выберет B 2 – мы ему ответим A 2 , и он отдаст 8 и т. д. Очевидно, осторожный противник должен выбрать ту стратегию, при которой наш максимальный выигрыш будет минимален .

Обозначим через β j максимальные значения в столбцах платежной матрицы (максимальный выигрыш игрока A , или, что то же самое, максимальный проигрыш игрока B ) для стратегии A i :

и добавим к матрице игры строку, содержащую эти значения:

Выбирая стратегию, противник предпочтет ту, для которой значение β j минимально. Обозначим его через β :

Величина β называется верхней ценой игры или минимаксом (минимум максимального выигрыша). Соответствующая минимаксу стратегия противника (игрока B ), называется минимаксной стратегией .

Минимакс – это значение выигрыша, больше которого заведомо не отдаст нам разумный противник (иначе говоря, разумный противник проиграет не больше, чем β ). В данном примере минимакс β равен 5 (соответствующая клетка в таблице выделена серым цветом) и достигается он при стратегии противника B 3 .

Итак, исходя из принципа осторожности («всегда рассчитывай на худшее!»), мы должны выбрать стратегию A 4 , а противник – стратегию B 3 . Принцип осторожности является в теории игр основным и называется принципом минимакса .

Рассмотрим пример 2 . Пусть игроки A и В одновременно и независимо друг от друга записывают одно из трех чисел: либо «1», либо «2», либо «3». Если сумма записанных чисел оказывается четной, то игрок B платит игроку A эту сумму. Если сумма нечетная, то эту сумму выплачивает игрок A игроку В .

Запишем платежную матрицу игры, и найдем нижнюю и верхнюю цены игры (номер стратегии соответствует записанному числу):

Игрок A должен придерживаться максиминной стратегии A 1 , чтобы выиграть не меньше –3 (то есть чтобы проиграть не больше 3). Минимаксная стратегия игрока B – любая из стратегий B 1 и B 2 , гарантирующая, что он отдаст не более 4.

Тот же самый результат мы получим, если будем записывать платежную матрицу с точки зрения игрока В . Фактически, эта матрица получается путем транспонирования матрицы, построенной с точки зрения игрока A , и изменения знаков элементов на противоположный (так как выигрыш игрока A – это проигрыш игрока В ):

Исходя из этой матрицы следует, что игрок B должен придерживаться любой из стратегий B 1 и B 2 (и тогда он проиграет не более 4), а игрок A – стратегии A 1 (и тогда он проиграет не более 3). Как видно, результат в точности совпадает с полученным выше, поэтому при анализе не важно, с точки зрения какого игрока мы его проводим.

8 ЧТО НАЗЫВАЕТСЯ ЦЕННОВОЙ ИГРОЙ.

9.В ЧЕМ СОСТОЙТ ПРИНЦЕП МИНИМАКСА.2. Нижняя и верхняя цена игры. Принцип минимакса

Рассмотрим матричную игру типа с платежной матрицей

Если игрок А выберет стратегию А i , то все его возможные выигрыши будут элементами i -й строки матрицы С . В наихудшем для игрока А случае, когда игрокВ применяет стратегию, соответствующую минимальному элементу этой строки, выигрыш игрока А будет равен числу .

Следовательно, для получения наибольшего выигрыша, игроку А нужно выбирать ту из стратегий, для которой число максимально .

Задача принятия решения, рассматриваемая в рамках системного подхода, содержит три основные компоненты: в ней выделены система, управляющая подсистема и среда. Теперь мы переходим к изучению задач принятия решения, в которых на систему воздействует не одна, а несколько управляющих подсистем, каждая из которых имеет свои цели и возможности действий. Такой подход к принятию решений называется теоретико-игровым, а математические модели соответствующих взаимодействий называются играми . Ввиду различия целей управляющих подсистем, а также определенных ограничений на возможности обмена информацией между ними, указанные взаимодействия носят конфликтный характер. Поэтому всякая игра представляет собой математическую модель конфликта. Ограничимся случаем, когда управляющих подсистем две. Если цели систем противоположны, конфликт называется антагонистическим, а математическая модель такого конфликта называется антагонистической игрой ..

В теоретико-игровой терминологии 1-я управляющая подсистема называется игроком 1 , 2-я управляющая подсистема - игроком 2 , множества

их альтернативных действий называются множествами стратегий этих игроков. Пусть Х - множество стратегий игрока 1, Y - множество стратегий

игрока 2. Состояние системы однозначно определяется выбором управляющих воздействий подсистемами 1 и 2, то есть выбором стратегий

x ∈X и y ∈Y . Пусть F (x ,y )- оценка полезности для игрока 1 того состояния

системы, в которое она переходит при выборе игроком 1 стратегии х и

игроком 2 стратегии у . Число F (x ,y ) называется выигрышем игрока 1 в ситуации (x ,y ), а функция F - функцией выигрыша игрока 1 . Выигрыш игрока

1 одновременно является проигрышем игрока 2 , то есть величиной, которую первый игрок стремится увеличить, а второй – уменьшить. Это и есть

проявление антагонистического характера конфликта: интересы игроков полностью противоположны (то, что выигрывает один, проигрывает другой).

Антагонистическую игру естественно задать системой Г= (Х, Y, F ).

Заметим, что формально антагонистическая игра задается фактически так же, как и задача принятия решения в условиях неопределенности - если

отождествить управляющую подсистему 2 со средой. Содержательное различие между управляющей подсистемой и средой состоит в том, что

поведение первой носит целенаправленный характер. Если при составлении математической модели реального конфликта у нас есть основание (или намерение) рассматривать среду как противника, цель которого - принести

нам максимальный вред, то такую ситуацию можно представить в виде антагонистической игры. Другими словами, антагонистическую игру можно трактовать как крайний случай ЗПР в условиях неопределенности,

характеризуемый тем, что среда рассматривается как противник, имеющий цель. При этом мы должны ограничить виды гипотез о поведении среды.

Наиболее обоснованной здесь является гипотеза крайней осторожности, когда, принимая решение, мы рассчитываем на самый худший для нас возможный вариант действий среды.

Определение. Если Х и Y конечны, то антагонистическая игра называется матричной. В матричной игре можно считать, что X ={1,…,n },

Y ={1,…,m } и положить aij=F (i,j ). Таким образом, матричная игра полностью определяется матрицей A= (aij ), i =1,…,n, j =1,…,m .

Пример 3.1. Игра с двумя пальцами.

Два человека одновременно показывают один или два пальца и называют число 1 или 2, означающее, по мнению говорящего, количество

пальцев, показанное другим. После того, как пальцы показаны и числа названы, происходит распределение выигрыша по следующим правилам:

если оба угадали или оба не угадали, сколько пальцев показал их соперник, выигрыш каждого равен нулю; если угадал только один, то противник платит угадавшему сумму денег, пропорциональную общему числу показанных

Это антагонистическая матричная игра. Каждый игрок имеет четыре стратегии: 1- показать 1 палец и назвать 1, 2- показать 1 палец и назвать 2, 3-

показать 2 пальца и назвать 1, 4 - показать 2 пальца и назвать 2. Тогда матрица выигрышей A=(aij), i= 1,…, 4, j= 1,…, 4 определяется следующим образом:

a12= 2, a21 = – 2, a13=a42= –3, a24=a31= 3, a34 = – 4, a43= 4,aij= 0 в остальных случаях.

Пример 3.2. Дискретная игра типа дуэли.

Задачами дуэльного типа описывается, например, борьба двух игроков,

каждый из которых желает совершить некое единовременное действие (выброс на рынок партии товара, заявка о покупке на аукционе) и выбирает для этого время. Пусть игроки продвигаются навстречу друг другу на n шагов. После каждого сделанного шага игрок может выстрелить или не выстрелить в противника. Выстрел может быть у каждого только один. Считается, что вероятность попасть в противника, если продвинуться на k n =5 имеет вид

Называется игра двух лиц с нулевой суммой, в которой в распоряжении каждого из них имеется конечное множество стратегий. Правила матричной игры определяет платёжная матрица, элементы которой - выигрыши первого игрока, которые являются также проигрышами второго игрока.

Матричная игра является антагонистической игрой. Первый игрок получает максимальный гарантированный (не зависящий от поведения второго игрока) выигрыш, равный цене игры, аналогично, второй игрок добивается минимального гарантированного проигрыша.

Под стратегией понимается совокупность правил (принципов), определяющих выбор варианта действий при каждом личном ходе игрока в зависимости от сложившейся ситуации.

Теперь обо всём по порядку и подробно.

Платёжная матрица, чистые стратегии, цена игры

В матричной игре её правила определяет платёжная матрица .

Рассмотрим игру, в которой имеются два участника: первый игрок и второй игрок. Пусть в распоряжении первого игрока имеется m чистых стратегий, а в распоряжении второго игрока - n чистых стратегий. Поскольку рассматривается игра, естественно, что в этой игре есть выигрыши и есть проигрыши.

В платёжной матрице элементами являются числа, выражающие выигрыши и проигрыши игроков. Выигрыши и проигрыши могут выражаться в пунктах, количестве денег или в других единицах.

Составим платёжную матрицу:

Если первый игрок выбирает i -ю чистую стратегию, а второй игрок - j -ю чистую стратегию, то выигрыш первого игрока составит a ij единиц, а проигрыш второго игрока - также a ij единиц.

Так как a ij + (- a ij ) = 0 , то описанная игра является матричной игрой с нулевой суммой.

Простейшим примером матричной игры может служить бросание монеты. Правила игры следующие. Первый и второй игроки бросают монету и в результате выпадает "орёл" или "решка". Если одновременно выпали "орёл" и "орёл" или "решка" или "решка", то первый игрок выиграет одну единицу, а в других случаях он же проиграет одну единицу (второй игрок выиграет одну единицу). Такие же две стратегии и в распоряжении второго игрока. Соответствующая платёжная матрица будет следующей:

Задача теории игр - определить выбор стратегии первого игрока, которая гарантировала бы ему максимальный средний выигрыш, а также выбор стратегии второго игрока, которая гарантировала бы ему максимальный средний проигрыш.

Как происходит выбор стратегии в матричной игре?

Вновь посмотрим на платёжную матрицу:

Сначала определим величину выигрыша первого игрока, если он использует i -ю чистую стратегию. Если первый игрок использует i -ю чистую стратегию, то логично предположить, что второй игрок будет использовать такую чистую стратегию, благодаря которой выигрыш первого игрока был бы минимальным. В свою очередь первый игрок будет использовать такую чистую стратегию, которая бы обеспечила ему максимальный выигрыш. Исходя из этих условий выигрыш первого игрока, который обозначим как v 1 , называется максиминным выигрышем или нижней ценой игры .

При для этих величин у первого игрока следует поступать следующим образом. Из каждой строки выписать значение минимального элемента и уже из них выбрать максимальный. Таким образом, выигрыш первого игрока будет максимальным из минимальных. Отсюда и название - максиминный выигрыш. Номер строки этого элемента и будет номером чистой стратегии, которую выбирает первый игрок.

Теперь определим величину проигрыша второго игрока, если он использует j -ю стратегию. В этом случае первый игрок использует такую свою чистую стратегию, при которой проигрыш второго игрока был бы максимальным. Второй игрок должен выбрать такую чистую стратегию, при которой его проигрыш был бы минимальным. Проигрыш второго игрока, который обозначим как v 2 , называется минимаксным проигрышем или верхней ценой игры .

При решении задач на цену игры и определение стратегии для определения этих величин у второго игрока следует поступать следующим образом. Из каждого столбца выписать значение максимального элемента и уже из них выбрать минимальный. Таким образом, проигрыш второго игрока будет минимальным из максимальных. Отсюда и название - минимаксный выигрыш. Номер столбца этого элемента и будет номером чистой стратегии, которую выбирает второй игрок. Если второй игрок использует "минимакс", то независимо от выбора стратегии первым игроком, он проиграет не более v 2 единиц.

Пример 1.

Наибольший из наименьших элементов строк - 2, это нижняя цена игры, ей соответствует первая строка, следовательно, максиминная стратегия первого игрока первая. Наименьший из наибольших элементов столбцов - 5, это верхняя цена игры, ей соответствует второй столбец, следовательно, минимаксная стратегия второго игрока - вторая.

Теперь, когда мы научились находить нижнюю и верхнюю цену игры, максиминную и минимаксную стратегии, пришло время научиться обозначать эти понятия формально.

Итак, гарантированный выигрыш первого игрока:

Первый игрок должен выбрать чистую стратегию, которая обеспечивала бы ему максимальный из минимальных выигрышей. Этот выигрыш (максимин) обозначается так:

Первый игрок использует такую свою чистую стратегию, чтобы проигрыш второго игрока был максимальным. Этот проигрыш обозначается так:

Второй игрок должен выбрать свою чистую стратегию так, чтобы его проигрыш был минимальным. Этот проигрыш (минимакс) обозначается так:

Ещё пример из этой же серии.

Пример 2. Дана матричная игра с платёжной матрицей

Определить максиминную стратегию первого игрока, минимаксную стратегию второго игрока, нижнюю и верхнюю цену игры.

Решение. Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим максимальный из них, а снизу от матрицы - наибольшие элементы в столбцах и выберем минимальный из них:

Наибольший из наименьших элементов строк - 3, это нижняя цена игры, ей соответствует вторая строка, следовательно, максиминная стратегия первого игрока вторая. Наименьший из наибольших элементов столбцов - 5, это верхняя цена игры, ей соответствует первый столбец, следовательно, минимаксная стратегия второго игрока - первая.

Седловая точка в матричных играх

Если верхняя и нижняя цена игры одинаковая, то считается, что матричная игра имеет седловую точку. Верно и обратное утверждение: если матричная игра имеет седловую точку, то верхняя и нижняя цены матричной игры одинаковы. Соответствующий элемент одновременно является наименьшим в строке и наибольшим в столбце и равен цене игры.

Таким образом, если , то - оптимальная чистая стратегия первого игрока, а - оптимальная чистая стратегия второго игрока. То есть равные между собой нижняя и верхняя цены игры достигаются на одной и той же паре стратегий.

В этом случае матричная игра имеет решение в чистых стратегиях .

Пример 3. Дана матричная игра с платёжной матрицей

Нижняя цена игры совпадает с верхней ценой игры. Таким образом, цена игры равна 5. То есть . Цена игры равна значению седловой точки . Максиминная стратегия первого игрока - вторая чистая стратегия, а минимаксная стратегия второго игрока - третья чистая стратегия. Данная матричная игра имеет решение в чистых стратегиях.

Решить задачу на матричную игру самостоятельно, а затем посмотреть решение

Пример 4. Дана матричная игра с платёжной матрицей

Найти нижнюю и верхнюю цену игры. Имеет ли данная матричная игра седловую точку?

Матричные игры с оптимальной смешанной стратегией

В большинстве случаев матричная игра не имеет седловой точки, поэтому соответствующая матричная игра не имеет решений в чистых стратегиях.

Но она имеет решение в оптимальных смешанных стратегиях. Для их нахождения нужно принять, что игра повторяется достаточное число раз, чтобы на основании опыта можно было предположить, какая стратегия является более предпочтительной. Поэтому решение связывается с понятием вероятности и среднего (математического ожидания). В окончательном же решении есть и аналог седловой точки (то есть равенства нижней и верхней цены игры), и аналог соответствующих им стратегий.

Итак, чтобы чтобы первый игрок получил максимальный средний выигрыш и чтобы средний проигрыш второго игрока был минимальным, чистые стратегии следует использовать с определённой вероятностью.

Если первый игрок использует чистые стратегии с вероятностями , то вектор называется смешанной стратегией первого игрока. Иначе говоря, это "смесь" чистых стратегий. При этом сумма этих вероятностей равна единице:

Если второй игрок использует чистые стратегии с вероятностями , то вектор называется смешанной стратегией второго игрока. При этом сумма этих вероятностей равна единице:

Если первый игрок использует смешанную стратегию p , а второй игрок - смешанную стратегию q , то имеет смысл математическое ожидание выигрыша первого игрока (проигрыша второго игрока). Чтобы его найти, нужно перемножить вектор смешанной стратении первого игрока (который будет матрицей из одной строки), платёжную матрицу и вектор смешанной стратегии второго игрока (который будет матрицей из одного столбца):

Пример 5. Дана матричная игра с платёжной матрицей

Определить математическое ожидание выигрыша первого игрока (проигрыша второго игрока), если смешанная стратегия первого игрока , а смешанная стратегия второго игрока .

Решение. Согласно формуле математического ожидания выигрыша первого игрока (проигрыша второго игрока) оно равно произведению вектора смешанной стратегии первого игрока, платёжной матрицы и вектора смешанной стратегии второго игрока:

первого игрока называется такая смешанная стратегия , которая обеспечивала бы ему максимальный средний выигрыш , если игра повторяется достаточное число раз.

Оптимальной смешанной стратегией второго игрока называется такая смешанная стратегия , которая обеспечивала бы ему минимальный средний проигрыш , если игра повторяется достаточное число раз.

По аналогии с обозначениями максимина и минимакса в случах чистых стратегий оптимальные смешанные стратегии обозначаются так (и увязываются с математическим ожиданием, то есть средним, выигрыша первого игрока и проигрыша второго игрока):

В таком случае для функции E существует седловая точка , что означает равенство .

Для того, чтобы найти оптимальные смешанные стратегии и седловую точку, то есть решить матричную игру в смешанных стратегиях , нужно свести матричную игру к задаче линейного программирования, то есть к оптимизационной задаче, и решить соответствующую задачу линейного программирования.

Сведение матричной игры к задаче линейного программирования

Для того, чтобы решить матричную игру в смешанных стратегиях, нужно составить прямую задачу линейного программирования и двойственную ей задачу . В двойственной задаче расширенная матрица, в которой хранятся коэффициенты при переменных в системе ограничений, свободные члены и коэффициенты при переменных в функции цели, транспонируется. При этом минимуму функции цели исходной задачи ставится в соответствие максимум в двойственной задаче.

Функция цели в прямой задаче линейного программирования:

Система ограничений в прямой задаче линейного программирования:

Функция цели в двойственной задаче:

Система ограничений в двойственной задаче:

Оптимальный план прямой задачи линейного программирования обозначим

а оптимальный план двойственной задачи обозначим

Линейные формы для соответствующих оптимальных планов обозначим и ,

а находить их нужно как суммы соответствующих координат оптимальных планов.

В соответствии определениям предыдущего параграфа и координатами оптимальных планов, в силе следующие смешанные стратегии первого и второго игроков:

Математики-теоретики доказали, что цена игры следующим образом выражается через линейные формы оптимальных планов:

то есть является величиной, обратной суммам координат оптимальных планов.

Нам, практикам, остаётся лишь использовать эту формулу для решения матричных игр в смешанных стратегиях. Как и формулы для нахождения оптимальных смешанных стратегий соответственно первого и второго игроков:

в которых вторые сомножители - векторы. Оптимальные смешанные стратегии также, как мы уже определили в предыдущем параграфе, являются векторами. Поэтому, умножив число (цену игры) на вектор (с координатами оптимальных планов) получим также вектор.

Пример 6. Дана матричная игра с платёжной матрицей

Найти цену игры V и оптимальные смешанные стратегии и .

Решение. Составляем соответствующую данной матричной игре задачу линейного программирования:

Получаем решение прямой задачи:

Находим линейную форму оптимальных планов как сумму найденных координат.

Подход к решению матричных игр может быть обобщен на случай антагонистических игр, в которых платеж игроков задается в виде непрерывной функции (бесконечная антагонистическая игра).

Такая игра представляется как игра двух игроков, в которой игрок 1 выбирает число х из множества X, игрок 2 выбирает число у из множества 7, и после этого игроки 1 и 2 получают соответственно выигрыши U (х, у) и -U(x, у). Выбор определенного числа игроком означает применение его чистой стратегии, соответствующей этому числу.

По аналогии с матричными играми чистой нижней ценой игры можно назвать v { = max min U(x, у), а чистой верхней ценой игры -v 2 =

min max U{x, у). Тогда по аналогии можно считать, что если для какой-

у *

либо бесконечной антагонистической игры величины V и v 2 существуют и равны между собой («i =v 2 =v), то такая игра имеет решение в чистых стратегиях, т.е. оптимальной стратегией игрока 1 является выбор числа х° е X, а игрока 2 - числа у 0 е 7, при которых Щх { у 0) -v.

В этом случае v называется чистой ценой игры, а (х°, у 0) - седловой точкой бесконечной антагонистической игры.

Для матричных игр величины v x и v 2 всегда существуют, но в бесконечных антагонистических играх они могут и не существовать, т.е. бесконечная антагонистическая игра не всегда разрешима.

При формализации реальной ситуации в виде бесконечной антагонистической игры обычно выбирается единичный стратегический интервал - единичный промежуток, из которого игроки могут сделать выбор (х - число (стратегия), выбираемое игроком 1; -

число (стратегия), выбираемое игроком 2). Технически это упрощает решение, так как простым преобразованием любой интервал можно перевести в единичный и наоборот. Такая игра называется антагонистической игрой на единичном квадрате.

Для примера допустим, что игрок 1 выбирает число х из множества Х= , игрок 2 выбирает число у из множества Y= . После этого игрок 2 платит игроку 1 сумму Щх, у) -2х 2 -у 2 . Поскольку игрок 2 стремится минимизировать платеж игрока 1, то он определяет min (2х 2 - у 2) = 2х 2 - 1, т.е. при этому= 1. Игрок 1 стремится мак- тег

симизировать свой платеж, поэтому определяет maxi min Щх, у)1 =

xGX у ег

- max (2х 2 - 1) = 2- 1 = 1, который достигается при х = 1.

Таким образом, нижняя чистая цена игры v x - 1. Верхняя чистая

цена игры v 2 = min - min (2 - у 2) = 2 - 1 = 1, т.е. в этой

>ег хех у еу

игре v l =v 2 =l. Поэтому чистая цена игры v = 1, а седловая точка (х° = 1; у°=1).

Предположим теперь, что Хи Y- открытые интервалы, т.е. игрок 1 выбираетxeA"=(0; 1), игрок 2 выбирает уе 7= (0; 1). В этом случае, выбирая х, достаточно близкое к 1, игрок 1 будет уверен, что он получит выигрыш не меньше, чем число, близкое к»=1; выбирая у, близкое к 1, игрок 2 не допустит, чтобы выигрыш игрока 1 значительно превышал чистую цену игры v= 1.

Степень близости к цене игры может характеризоваться числом?>0. Поэтому в описываемой игре можно говорить об оптимальности чистых стратегий х° = 1, у 0 = 1 соответственно игроков 1 и 2 с точностью до произвольного числа?>0. Точка (х„ , у Е), где х е е X, у (. eY, в бесконечной антагонистической игре называется точкой z-равновесия (с.-седловой точкой) , если для любых стратегий хеТигрока 1,уе Тигро- ка 2 имеет место неравенство Щх, у.) - ? Щ x r , у (.) U(x t ., у) + ?. В этом случае стратегии х к. и у. называются с,-оптимальными стратегиями . Эти стратегии являются оптимальными с точностью до? в том смысле, что если отклонение от оптимальной стратегии никакой пользы игроку принести не может, то его отклонение от с-оптимальной стратегии может увеличить его выигрыш не более чем на е.

Если игра не имеет седловой точки (с-седловой точки), т.е. решения в чистых стратегиях, то оптимальные стратегии можно искать среди смешанных стратегий, в качестве которых используются функции распределения вероятностей применения игроками чистых стратегий.

Пусть F(x) - функция распределения вероятностей применения чистых стратегий игроком 1. Если число Е, - чистая стратегия игрока 1, то F(x) = P(q где P(q - Х) - вероятность того, что случайно выбранная чистая стратегия Е, не будет превосходить х. Аналогично рассматривается функция распределения вероятностей применения чистых стратегий г| игроком 2: Q(y) = Р(г .

Функции F(x) и Q(y) называются смешанными стратегиями соответственно игроков 1 и 2. Если Fx) и Q(y) дифференцируемы, то существуют их производные, обозначаемые соответственно через f{x) и q(y) (функции плотности распределения).

В общем случае дифференциал функции распределения dF{x ) выражает вероятность того, что стратегия с, находится в промежутке х Е, Аналогично для игрока 2: dQ(y) означает вероятность того, что его стратегия р находится в интервале у г| у+dy. Тогда платеж игрока 1 составит Щх, у) dF(x), а платеж игрока 2 равен Щх, у) dQ(y).

Средний платеж игрока 1 при условии, что игрок 2 применяет свою чистую стратегию у, можно получить, проинтегрировав платежи по всем возможным значениям х, т.е. на единичном интервале:

Средний платеж игрока 1 при условии, что оба игрока применяют свои смешанные стратегии F{x) и Q(y), будет равен

По аналогии с матричными играми определяются оптимальные смешанные стратегии игроков и цена игры: если пара смешанных стратегий F*(x ) и Q*(y) соответственно для игроков 1 и 2 являются оптимальными, то для любых смешанных стратегий F(x) и Q(y) справедливы соотношения:

Если игрок 1 отступает от своей стратегии F*(x), то его средний выигрыш не может увеличиться, но может уменьшиться из-за рациональных действий игрока 2. Если игрок 2 отступит от своей смешанной стратегии Q*(y), то средний выигрыш игрока 1 может увеличиться, но не уменьшиться, за счет более разумных действий игрока 1. Средний выигрыш E(F*, Q*), получаемый игроком 1 при применении игроками оптимальных смешанных стратегий, соответствует цене игры.

Тогда нижняя цена бесконечной антагонистической игры, решаемой в смешанных стратегиях, может быть определена как v x = шах

min Е (FQ), а верхняя цена игры как v 2 = min max Е(F, Q).

Q Q f

Если существуют такие смешанные стратегии F* (х) и Q* (у) соответственно для игроков 1 и 2, при которых нижняя и верхняя цены игры совпадают, то F*(x) и Q*(y) естественно назвать оптимальными смешанными стратегиями соответствующих игроков, a v=v x = v 2 - ценой игры.

В отличие от матричных игр решение бесконечной антагонистической игры существует не для всякой функции Щх, у). Но доказана теорема о том, что всякая бесконечная антагонистическая игра с непрерывной платежной функцией Щх, у) на единичном квадрате имеет решение (игроки имеют оптимальные смешанные стратегии), хотя общих методов для решения бесконечных антагонистических игр, в том числе непрерывных игр, не существует. Однако достаточно просто решаются антагонистические бесконечные игры с выпуклыми и вогнутыми непрерывными платежными функциями (они называются соответственно выпуклыми и вогнутыми играми).

Рассмотрим решение игр с выпуклой платежной функцией. Решение игр с вогнутой функцией выигрыша симметрично.

Выпуклой функцией/переменной х на интервале (а ; Ь) называется такая функция, для которой выполняется неравенство

где Хх и х 2 - любые две точки из интервала (а; b );

Х.1, А.2 > 0, причем +Х.2= 1.

Если для / ч * 0 Д 2 * 0, всегда имеет место строгое неравенство

то функция/называется строго выпуклой на (а; Ь).

Геометрически выпуклая функция изображает дугу, график которой расположен ниже стягивающей ее хорды. Аналитически выпуклость дважды дифференцируемой функции соответствует неотрицательности (а в случае строгой выпуклости - положительности) ее второй производной.

Для вогнутых функций свойства противоположны, для них должно выполняться неравенство/(/4X1 +А.2Х2) > Kf (xi) +)-if (х 2) (> при строгой вогнутости), а вторая производная/"(х)

Доказано , что непрерывная и строго выпуклая функция на замкнутом интервале принимает минимальное значение только в одной точке интервала. Если Щх, у) - непрерывная функция выигрышей игрока 1 на единичном квадрате и строго выпуклая по у для любого х, то имеется единственная оптимальная чистая стратегия у=у° е для игрока 2, цена игры определяется по формуле

а значение у 0 определяется как решение следующего уравнения:

Если функция Щх, у) не строго выпуклая по у, то у игрока 2 оптимальная чистая стратегия не будет единственной.

Симметричное свойство выполняется и для строго вогнутых функций. Если функция Щх, у) непрерывна по обоим аргументам и строго вогнута по х при любом у, то игрок 1 имеет единственную оптимальную стратегию.

Цена игры определяется по формуле

а чистая оптимальная стратегия х 0 игрока 1 определяется из уравнения

На основании этих свойств бесконечных антагонистических игр с выпуклой или вогнутой функциями выигрыша построена общая схема решения таких игр на единичном квадрате (х е , у е ). Приведем эту схему лишь для выпуклых игр , поскольку для вогнутых игр она симметрична.

1. Проверить функцию Щх, у) на выпуклость по у (вторая частная производная должна быть больше либо равна 0).

2. Определить у 0 из соотношения v- min max Щх, у) как значение

у, на котором достигается минимакс.

3. Найти решение уравнения v = U(x, у 0) и составить пары его решений Х и х 2 , для которых

4. Найти параметр а из уравнения

Параметр а определяет оптимальную стратегию игрока 1 и имеет смысл вероятности выбора им его чистой стратегии х х. Величина 1 - а имеет смысл вероятности выбора игроком 1 его чистой стратегии х 2 .

Покажем на примере использование этой схемы для решения игры такого вида. Пусть функция выигрыша в бесконечной антагонистической игре задана на единичном квадрате и равна Щх, у) = = (х - у) 2 =х 2 - 2ху ч-у 2 .

1. Эта функция непрерывна по х и у, и поэтому эта игра имеет решение. Функция Щх, у) строго выпукла по у, так как

Следовательно, игрок 2 имеет единственную чистую оптимальную стратегию у 0 .

2. Имеем v = min max (х - у) 2 . Для определения max (х 2 - 2ху Ч-у 2)

последовательно найдем первую и вторую частные производные пла- тежной функции по х:

Таким образом, функция U имеет минимум для любого у при х=у. Это значит, что при ху - возрастает, а ее максимум должен достигаться в одной из крайних точек х=0 или х= 1. Определим значения функции U в этих точках:

Тогда шах (х - у) 2 = тах {у 2 ; 1 - 2у+у 2 }. Сравнивая «внутренние»

максимумы, стоящие в фигурных скобках, легко заметить, что у 2 > 1 - - 2у+у 2 , если у > */ 2 и у 2 1 - 2у+у 2 , если у "/ 2 . Более наглядно это представляется графиком (рис. 2.5).

Рис. 2.5. Внутренние максимумы платежной функции U(х, у) = (х- у ) 2

Поэтому выражение (х - у) 2 достигает своего максимума при х=0, если у > 7 2 , и при х= 1, если у У 2:

Следовательно, v= min { min у 2 ; min (1 - у) 2 }. Каждый из вну-

тренних минимумов достигается при у= */ 2 и принимает значение У 4 . Таким образом, цена игры г = У 4 , а оптимальная стратегия игрока 2:

3. Определим оптимальную стратегию игрока 1 из уравнения U(x, у 0)=v, т.е. для данной игры (х - У 2) 2 =У 4 . Решением этого уравнения ЯВЛЯЮТСЯ Х| =0, х 2 = 1.

Для них выполняются условия

4. Определим параметр а, т.е. вероятность применения игроком 1 его чистой стратегии Х] = 0. Составим уравнение а-1 + (1 - а) (-1)=0, откуда а = У 2 . Таким образом, оптимальная стратегия игрока 1 состоит в выборе им своих чистых стратегий 0 и 1 с вероятностью 1 / 2 каждая. Задача решена.